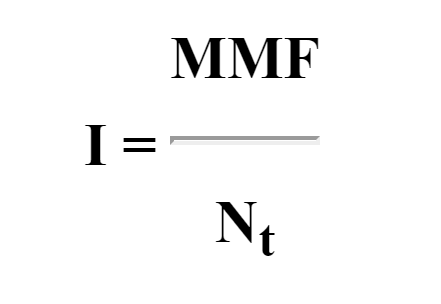The online magnetic calculator from International Magnetic Solutions generates graphs of magnetic flux density (induction). The program demonstrates the results of several approximate formulae used to estimate magnetic flux density, attractive force etc. This is the list of calculation cases currently documented:
To estimate the flux density B on the central axis at a distance x from the magnet, we use the formula:
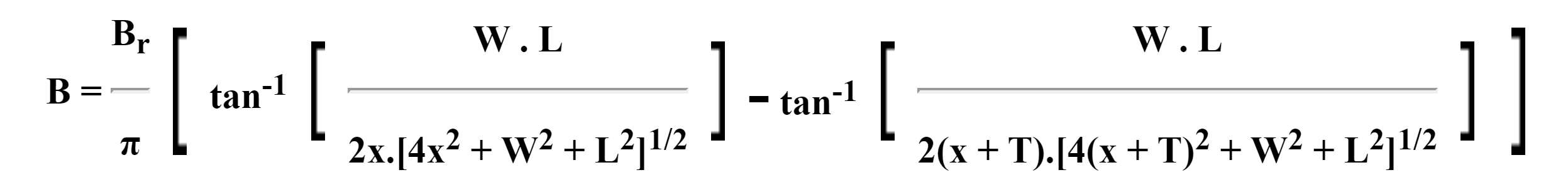
To estimate the flux density B on the central axis at a distance x from the magnet, we use the formula:
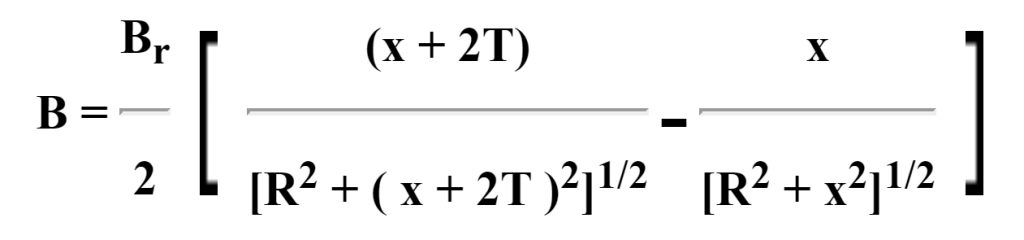
To estimate the flux density B on the central axis at a distance x from the magnet, we use the formula below. This is equivalent to the single rectangular magnet case using double the thickness of the magnet to simulate the effect of the steel – a common approximation.
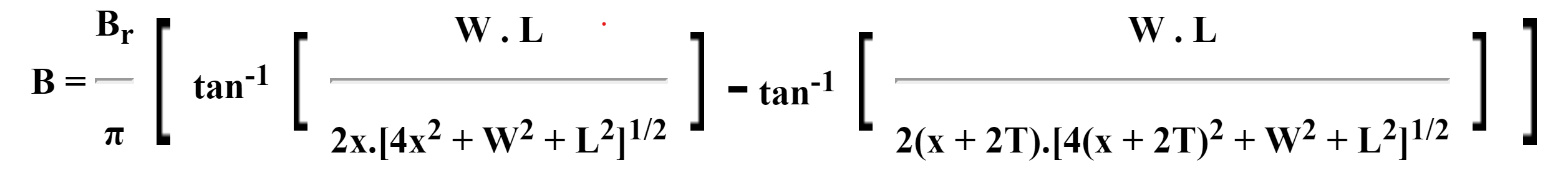
To estimate the flux density B on the central axis at a distance x from the magnet, we use the formula below. This is equivalent to the single rod magnet case using double the thickness of the magnet to simulate the effect of the steel – a common approximation.
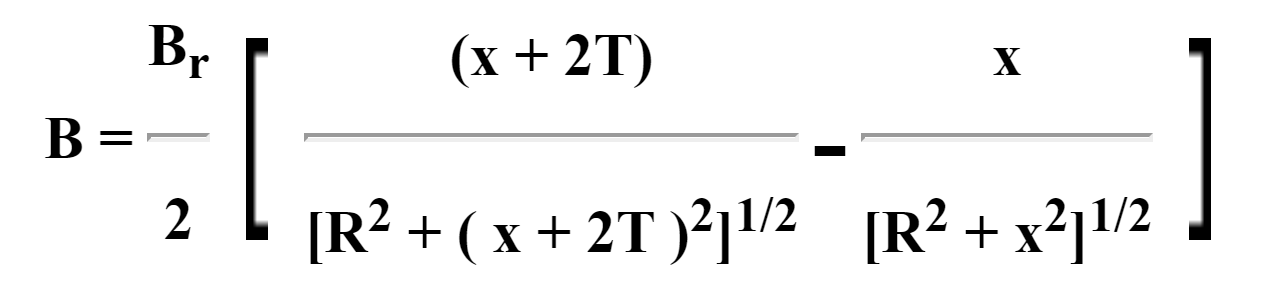

This applies to the four cases above, ie. Single rectangular or rod magnets, with or without steel backing.
To estimate the flux density B on the central axis at a distance x from the magnet, we use the relevant formula above as for a solid magnet and then subtract the value of flux density calculated for a magnet the shape and dimensions of the hole.
Note that this calculation generally results in a negative value of flux density close to the magnet, indicating flux reversal in this region on the axis. Because of the rapid variation of flux density off the axis great care should be taken when attempting to make use of these results.
To estimate the flux density B on the central axis at a distance x from the centre point, we use the formula below. This is derived from the single rectangular magnet formula using the principle of superposition.
B = B1 + B2
where B1 is the flux density for a rectangular block at distance x1 = (d/2 + x), B2 is the flux density for a rectangular block at distance x2 = (d/2 – x), d being the distance between the magnets.
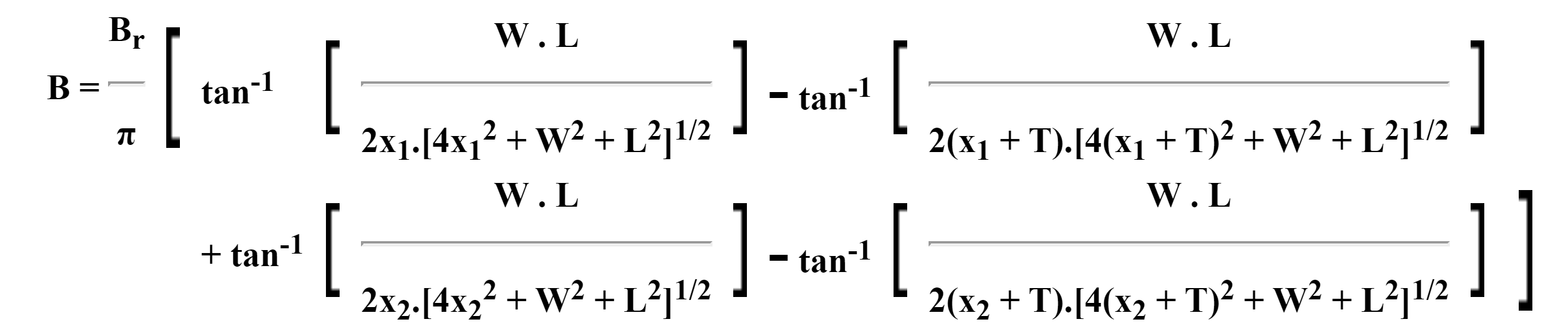
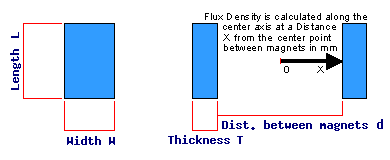
To estimate the flux density B on the central axis at a distance x from the centre point, we use the formula below. This is derived from the single rod magnet formula using the principle of superposition.
B = B1 + B2
where B1 is the flux density for a rectangular block at distance x1 = (d/2 + x), B2 is the flux density for a rectangular block at distance x2 = (d/2 – x), d being the distance between the magnets.
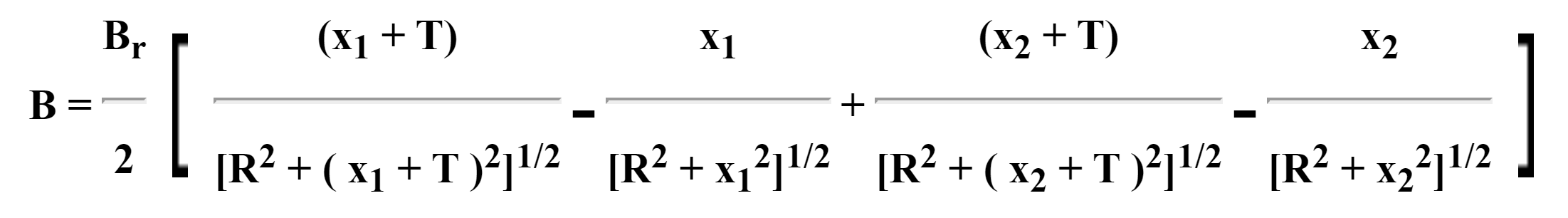
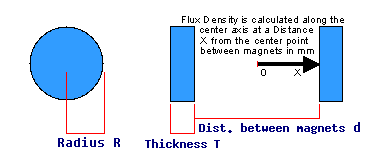
To estimate the flux density B on the central axis at a distance x from the centre point, we use the formula below.
Using an approximation, the results of the earlier analysis of 2 rectangular magnets facing each other can be applied to magnets in a steel circuit provided that the steel is not saturated. When using these formulas, it is customary to double the thickness of the magnet to simulate the effect of the steel. If most of the flux is passing through the gap (i.e. not leaking to nearby magnets and steel), this is a good approximation.
As before, we use the principle of superposition.
B = B1 + B2
where B1 is the flux density for a rectangular block at distance x1 = (d/2 + x), B2 is the flux density for a rectangular block at distance x2 = (d/2 – x), d being the distance between the magnets.

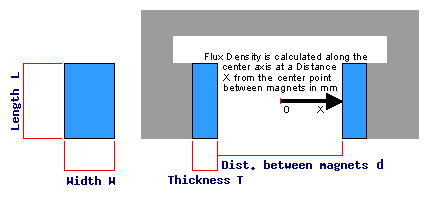
To estimate the flux density B on the central axis at a distance x from the centre point, we use the formula below.
Using an approximation, the results of the earlier analysis of 2 rod magnets facing each other can be applied to magnets in a steel circuit provided that the steel is not saturated. When using these formulas, it is customary to double the thickness of the magnet to simulate the effect of the steel. If most of the flux is passing through the gap (i.e. not leaking to nearby magnets and steel), this is a good approximation.
As before, we use the principle of superposition.
B = B1 + B2
where B1 is the flux density for a rectangular block at distance x1 = (d/2 + x), B2 is the flux density for a rectangular block at distance x2 = (d/2 – x), d being the distance between the magnets.
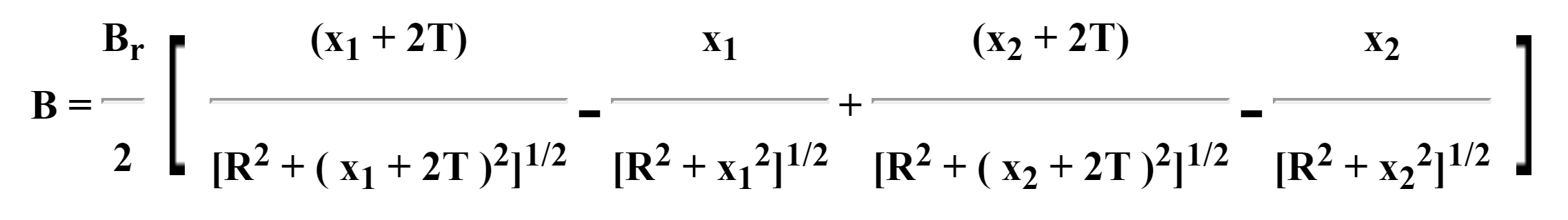
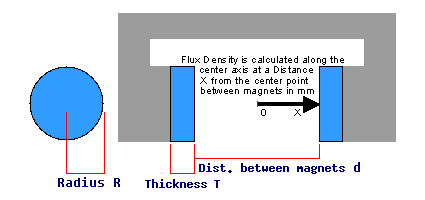
This applies to the four cases above, ie. Single rectangular or rod magnets, with or without steel backing.
To estimate the force F on a large piece of steel at a distance x from the magnet, we calculate the cross-sectional area of the magnet A, and use the relevant formula above to calculate the flux density B on the axis for a solid magnet.
Where a steel backing is NOT used, we also apply a special case where x=0 (steel in contact with magnet) and use the formula for a steel-backed magnet.
Then the following empirical formula gives an approximate estimate of the force:
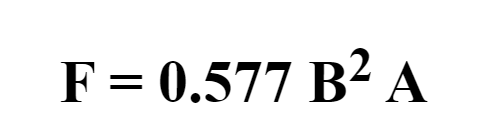

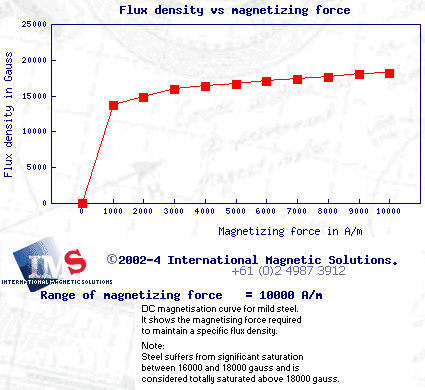
This case simply plots a section from our digitized magnetic material property data for steel. The same data is also used in other calculations, below.
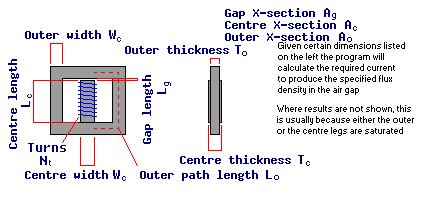 This case concerns a 3-leg magnetic circuit with an electrical coil wound around the centre leg. We estimate the current required in the coil to achieve a given flux density in the gap.
This case concerns a 3-leg magnetic circuit with an electrical coil wound around the centre leg. We estimate the current required in the coil to achieve a given flux density in the gap.
First we calculate the cross-sectional areas of the centre and outer legs Ac and Ao from the specified width and thickness values. The cross-sectional area of the gap Ag is either taken to be equal to that of the centre leg or is specified by the user, depending on the analysis case.
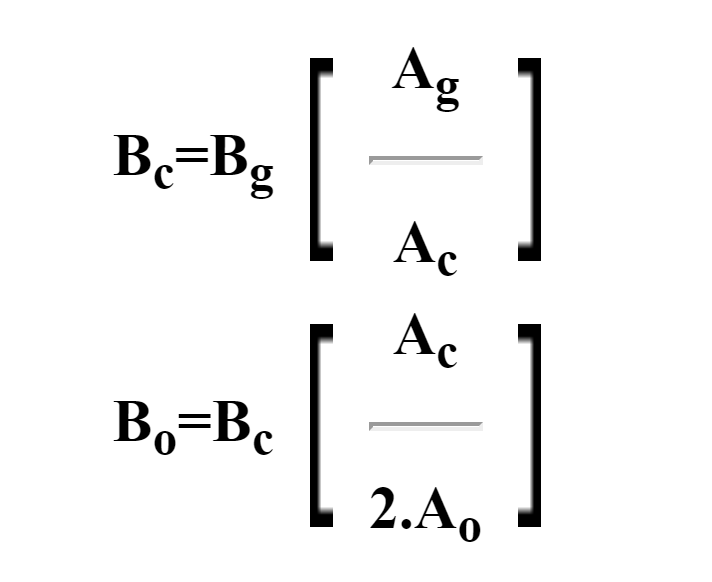
Then we use the following formulae to calculate flux density in the centre and outer legs Bc and Bo (Bg is the required flux in the gap, specified by the user).
Next we calculate the magnetizing forces in the centre and outer legs MFc and MFo by lookups in the digitized material property data for steel (see Flux density vs magnetizing force for mild steel material above). The magnetizing force in the air gap MFg comes directly from the permeability of air μ0:
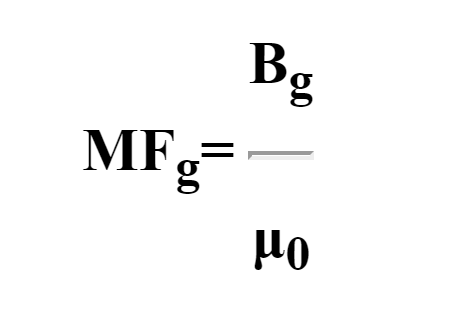
We multiply the magnetizing force in each part of the circuit by its length to obtain the magneto-motive force (MMF) and sum this to obtain the total MMF in the circuit:

Finally, the current in the coil I is the MMF divided by the number of turns Nt: